It all started a few months ago when I created a quad-tree structure and then wanted to be able to visualize those trees with GraphViz. Thus this tree meditation was born. And who was the master of happy little trees? Bob Ross of course. So if you like, read the following in Bob’s very relaxing voice…. try not to go to sleep.

Before we can code our happy little trees we need to define what a tree is:

1

# type 'a tree = Empty | Leaf of 'a | Node of 'a tree * 'a * 'a tree ;;

You can go ahead and type that yourself into the online OCaml REPL (Read Evaluate Print Loop). Go ahead, give it a try.

The type definition here is in OCaml. The ML family of languages (SML, OCaml and Haskell, for example) excel at creating pretty trees because they have algebraic data types. What’s the ‘a tree mean? The ‘a is a type variable and means that we’re creating trees which contain data of type ‘a. Since ‘a isn’t specified it means that any type of data could live in the tree; our tree is polymorphic.

Since this is a SUM type (also called an OR type, notice the ‘|’s in the definition above) we can surmise that a tree can either be Empty or have a Leaf or a Node. Empty, Leaf and Node are used to build our tree, they are our tree constructors.

Empty, what’s that mean? Think of it as the tree of nothingness. Very Zen. Hopefully it will make more sense when we start creating and traversing trees.

Leaf of ‘a means that a leaf can contain data of type ‘a and as was explained above, that means that the leaf can contain data of any type. How do we create a Leaf of ‘a in our code?

1
2

# Leaf "I'm a Leaf" ;;
- : string tree = Leaf "I'm a Leaf" 

The above was typed into the OCaml REPL. The # is the REPL prompt, we only typed in the actual Leaf “I’m a Leaf” part. The second line shows the result. Notce that the type is string tree because we passed a string to the Leaf constructor. So our leaf is itself a tree. Ok, maybe that seems a little stange, but hold up a leaf by the stem and it can certainly look like a little tree on it’s own, don’t you think? Fractals, think fractals.

Now we’re left with that *Node of ‘a tree * ‘a * ‘a tree* part of the tree type definition. Here we’ve reached the essence of treeness. A Node of a tree has three parts: A ‘a tree on the left, the actual ‘a data contained by this Node and another ‘a tree on the right. This part of the definition of tree is recursive because a Node is the piece of a tree which can contain other trees - in our case we have defined a binary tree type since each node has only two branches: a left tree and a right tree. What’s with the asterisks? Technically they indicate that this part of the type is a Cartesian product (algebraic datatypes remember). We can think of this particular one as a triple - a collection of 3 things.

So without further ado, let’s code a happy little tree:

1
2

# Node(Leaf 2, 1, Leaf 3) ;;
- : int tree = Node (Leaf 2, 1, Leaf 3)

The REPL tells us this is an int tree, a tree which contains integers at it’s nodes and leaves.

And what does it look like?

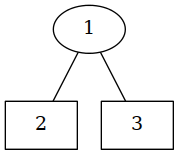
Notice in this case that we’ve got a complete tree; we did not use the Empty constructor. What if we had?

1
2

# Node(Leaf 2, 1, Empty) ;;
- : int tree = Node (Leaf 2, 1, Empty)

Now we have what is perhaps a less happy little tree. The right branch of our little tree is empty. The Leaf 3 has fallen. Now perhaps you can see why we need Empty. Node must have two sub-trees. We can’t just do something like:

1
2
3
4

# Node(Leaf 2, 1) ;;
File "", line 1, characters 1-16:
Error: The constructor Node expects 3 argument(s),
       but is applied here to 2 argument(s)

Because the Node constructor expects to have three components. So Empty is used to designate the absense of a Node or Leaf.

How did I draw that tree above? That’ll have to wait for the next Tree Medititation installment when we’ll discuss things like tree traversal and generating dot files used by Graphviz to create images.